TWI: Ermüdungsanalyse

Deutsche Übersetzung von Stephan Kallee^<1> der englischen Veröffentlichung von Hadi Khalili^<2><3>*, Selda Oterkus^<2>* Nigel Barltrop^<2> und Ujjwal Bharadwaj^<4>: Updating the Distributions of Uncertain Parameters Involved in Fatigue Analysis

<1> AluStir, Im Unterdorf 19, 63826 Geiselbach, Germany

<2> Department of Naval Architecture, Ocean & Marine Engineering, University of Strathclyde, Glasgow G4 0LZ, UK

<3> National Structural Integrity Research Centre, TWI Ltd, Granta Park, Cambridge CB21 6AL, UK
<4> TWI Ltd., Granta Park, Great Abington, Cambridge CB21 6AL, UK

*Korrespondierende Autorin: selda.oterkus@strath.ac.uk; Tel.: +44-141-548-4979

Auf Englisch erstveröffentlicht in der Spezialausgabe 'Offshore and Subsea Structures' des 'Journal of Marine Science and Engineering'

J. Mar. Sci. Eng. 2020, 8(10), 778; DOI: https://www.mdpi.com/2077-1312/8/10/778

Englisches Original erhalten: 8. September 2020, überarbeitet: 30. September 2020, freigegeben: 2. Oktober 2020, publiziert: 4. Oktober 2020. Deutsche Übersetzung erstellt: 3. Januar 2021.

Transport einer Jacket-Plattform für das Offshore-Umspannwerk 'Borkum Riffgrund 2'

© Kees Torn, CC BY-SA 2.0

Materialermüdung ist ein wichtiger Ausfallmodus bei Offshore-Jacket-Plattformen. Um die Ermüdungsschäden zu bewerten, werden diese Plattformen während ihrer Lebensdauer regelmäßig inspiziert. In Bezug auf Ermüdungsschäden bestehen die Informationen aus der Inspektion aus der Rissmessung. Ein Bayes'scher Rahmen kann verwendet werden, um die Wahrscheinlichkeitsverteilung der Rissgröße zu aktualisieren. Das Hauptziel dieser Studie ist die Entwicklung eines Rahmens zur Aktualisierung der Wahrscheinlichkeitsverteilungen aller unsicheren Parameter, die an der Analyse des Ermüdungsrisswachstums beteiligt sind. Diese Methodik maximiert den Nutzen der Prüfergebnisse durch die Aktualisierung mehrerer unsicherer Parameter, die in den bruchmechanischen Ansatz involviert sind. Zwei Sätze von Rissen werden verwendet, um die aktualisierten Verteilungen für unsichere Parameter zu erhalten; A-priori-Risse und Simulierte-Realitäts-Risse. Durch den Vergleich dieser Risse erhält man die aktualisierten Verteilungen für die unsicheren Parameter. Die aktualisierte Rissgrößenverteilung kann verwendet werden, um die Schätzung der Versagens­wahrscheinlich­keit zu aktualisieren. Um das entwickelte Rahmenwerk zu demonstrieren, wird eine rohrförmige Verbindung in einer spezifischen Jacket-Plattform betrachtet und das Rahmenwerk wird für diese Verbindung angewendet. Die Ergebnisse der entwickelten Methodik zeigen, dass sich die aktualisierten Verteilungen der unsicheren Parameter in Richtung der Simulierte-Realitäts-Verteilungen verschieben.

Schlüsselwörter: Ermüdungsrissgröße; Offshore-Jacket-Plattformen; rohrförmige Verbindung; Bruchmechanik; Unsicherheit; Inspektionsergebnisse

Weblinks (Wikipedia): Bayes'sche Statistik, Simulierte Realität, A-priori-Wahrscheinlich­keit, Likelihood-Funktion

Offshore-Jacket-Plattformen sind häufig verwendete Strukturen für die Öl- und Gasförderung in rauen Umgebungen. Jacket-Plattformen sind aufgrund von drei Hauptgründen anfällig für Ermüdungsschäden: hohe Spannungskonzentrationen an den Schnittpunkten, Defekte während des Schweißprozesses und zyklische Wellenbelastung, die auf die Struktur einwirken. Aufgrund der Idealisierungen und Näherungen in der Ermüdungsanalyse, der Existenz vieler Unsicherheiten in den Belastungen, die auf solche Strukturen einwirken, und der Widerstandsfähigkeit der Struktur, ist ein probabilistischer Ansatz für die Durchführung der Ermüdungsanalyse eine rationale und konsistente Grundlage für die Einbeziehung von Unsicherheiten.

Ermüdungsschäden akkumulieren während der Lebensdauer der Struktur, wenn die Rissgröße zunimmt. Die Akkumulation von Schäden führt zu einer Verschlechterung der Strukturfestigkeit und erhöht die Wahrscheinlichkeit eines Versagens. Um den Zustand der Schäden zu beurteilen, werden Offshore-Plattformen periodisch inspiziert. In Bezug auf Ermüdungsschäden beinhalten die Informationen aus der Inspektion die Erkennung und Messung von Rissgrößen. Nach einer Inspektion einer Struktur kann die Wahrnehmung des Strukturzustands verbessert werden. Im Allgemeinen wird ein Bayes'scher Rahmen verwendet, um die Wahrscheinlichkeitsverteilungen der Unsicherheiten wie z. B. der Rissgröße zu aktualisieren. Der Zweck der Aktualisierung ist es, die Inspektionsergebnisse in eine verbesserte Schätzung des unsicheren Parameters einzubeziehen. Nach der Aktualisierung der Verteilung der Rissgröße ist es möglich, die Schätzung der Ausfallwahrscheinlichkeit der Komponente zu aktualisieren.

Es wurden mehrere Studien durchgeführt, um die Inspektionsinformationen zur Aktualisierung der Ermüdungsrissgrößenverteilung einzubeziehen. Heredia und Montes [1] entwickelten einen Bayes'schen Rahmen zur Aktualisierung der Wahrscheinlichkeitsverteilung der Rissgröße in Rohrverbindungen unter Verwendung der Informationen aus Inspektionsberichten. Zu diesem Zweck führten sie ein Fehlermodell ein, das eine logarithmische Differenz zwischen der gemessenen Rissgröße und der vorhergesagten Rissgröße darstellt. Sie verwendeten den Ansatz der Bruchmechanik, um die Rissgröße vorherzusagen. Für das Fehlermodell wurde eine Normalverteilung mit bekanntem Mittelwert und unsicherer Varianz angenommen. Daher wurde eine konjugierte Verteilung für die Fehlervarianz angenommen. Basierend auf diesen Annahmen präsentierten sie einen Ausdruck in geschlossener Form, um die Wahrscheinlichkeitsverteilung der Rissgröße in einer rohrförmigen Verbindung zu aktualisieren [1].

Karandikar et al. [2] führten eine Bayes'sche Inferenz unter Verwendung einer Random-Walk-Methode durch, um die verbleibende Lebensdauer eines Flugzeugrumpfpaneels vorherzusagen, das wiederholten Lastzyklen ausgesetzt ist. Sie betrachteten die Risswachstumsparameter und die anfängliche Rissgröße als unsichere Parameter. Sie generierten eine große Anzahl von Zufallsstichproben für die unsicheren Parameter, um die Ermüdungsrisswachstumskurve zu erzeugen. Die Wahrscheinlichkeit, dass jeder Stichprobenpfad die wahre Risswachstumskurve ist, wurde als Kehrwert der Anzahl der Stichproben angenommen, d.h. sie betrachteten eine Gleichverteilung für die Abschätzung der A-priori-Wahrscheinlichkeit (auch Anfangswahrscheinlichkeit, Vortest- oder Ursprungswahrscheinlichkeit). Die Likelihood-Funktion (auch Plausibilitätsfunktion oder Mutmaßlichkeitsfunktion) wurde als Normalverteilung dargestellt, um zu beschreiben, wie wahrscheinlich es ist, dass die Ermüdungsrisswachstumskurve genau dargestellt wird. Nachdem sie die Prior- und Likelihood-Funktion erhalten hatten, erhielten sie die posteriore Verteilung der Ermüdungsrissgröße [2].

Peng et al. [3] schlugen einen Bayes'schen Rahmen für eine probabilistische Ermüdungsprognose unter zyklischer Belastung vor. Für die Analyse des Ermüdungsrisswachstums wurde ein äquivalentes Spannungsniveau-Modell berücksichtigt. Sie führten Ermüdungstests unter Verwendung vorinstallierter piezoelektrischer Sensoren durch, um experimentelle Daten zu erhalten. Signalverarbeitungstechniken wurden verwendet, um die Risslänge abzuschätzen. Es wurden Vorverteilungen für die anfängliche Rissgröße, den Spannungsintensitätsfaktor und die Materialeigenschaften angenommen. Sie aktualisierten diese Verteilungen unter Verwendung des entwickelten Bayes'schen Rahmens, indem sie die Labortestergebnisse einbeziehen [3].

Carr et al. [4] entwickelten ein probabilistisches Modell zur Vorhersage der Ermüdungslebensdauer einer rohrförmigen Verbindung. Die Inspektionsergebnisse wurden bei der Analyse mit Hilfe der Bayes'schen Methoden ebenfalls berücksichtigt. Sie verwendeten die Inspektionsergebnisse, um schrittweise alle anfänglichen Unsicherheiten zu reduzieren. Die berücksichtigten Unsicherheiten in ihrer Studie waren die vorhergesagten Ermüdungslebensdauern der Verbindungen, die Erkennungswahrscheinlichkeitskurve und die Unsicherheiten im S-N-Ansatz (Wöhlerkurve) [4].

Das Hauptziel dieser Studie ist es, einen Rahmen für das Unsicherheitsmanagement von Rohrverbindungen unter Ermüdungsbelastung vorzuschlagen und zu demonstrieren. Das vorgeschlagene Rahmenwerk soll die prioren Annahmen mit Beobachtungen kombinieren, um die posterioren Schätzungen zu verbessern. In dieser Studie werden anstelle von realen Daten die Daten der Simulierten Realität verwendet, da die realen Daten in der Regel nicht ausreichend sind, um das Verhalten der Methode zu überprüfen.

Es ist erwähnenswert, dass verschiedene Empfehlungen unterschiedliche Prioritätsverteilungen für die unsicheren Parameter einführen, die an der Risswachstumsanalyse beteiligt sind. Die vorgeschlagenen Verteilungen basieren auf den experimentellen Tests. Zum Beispiel schlägt DNV [5] eine Exponentialverteilung für die Anfangsrissgröße vor, während JCSS [6] eine Lognormalverteilung vorschlägt. Die Anfangsrissgröße ist eine wichtige Variable, die die Ermüdungsrissgröße eines Bauteils beeinflusst [5]. Daher ist es entscheidend, eine geeignete Verteilung für diese unsicheren Parameter zu wählen. Der betrachtete Rahmen wird entwickelt, um die Verteilungen der unsicheren Parameter zu verbessern, wenn neue Informationen verfügbar werden, sowie die Rissgrößenverteilung zu aktualisieren.

In dieser Studie wird die Analyse der Ermüdungszuverlässigkeit basierend auf dem Bruchmechanik-Ansatz (Fracture Mechanics, FM) durchgeführt. Drei verschiedene Kategorien von Unsicherheiten werden mit der vorgeschlagenen Methodik aktualisiert, und zwar:

• Ermüdungsrissgröße
• Kurve der Entdeckungswahrscheinlichkeit (Probability of Detection, POD)
• Unsicherheiten, die im Bruchmechanik-Ansatz zur Vorhersage der Ermüdungsrissgröße enthalten sind (z. B. anfängliche Rissgröße, Risswachstumsparameter usw.)

Wenn zusätzliche Informationen, wie z. B. Inspektionsergebnisse, verfügbar werden, können die zusätzlichen Informationen verwendet werden, um die Prior-Schätzungen der unsicheren Parameter zu verbessern. Der Rahmen für die Aktualisierung der Verteilung der geschätzten Parameter wird als Bayes'scher Rahmen bezeichnet [7]. Die Verteilung, die das Vorwissen über den unsicheren Parameter beschreibt, wird als Prior-Verteilung (kurz für A-priori-Verteilung) bezeichnet [8]. Aufgrund der Unsicherheiten im Ermüdungsphänomen werden die neuen Informationen verwendet, um die Prior-Verteilungen der ungewissen Parameter zu verbessern [2].
    

Im Bayes'schen Rahmen werden für die Aktualisierung der Wahrscheinlichkeitsverteilungen der unsicheren Parameter zwei Sätze von Informationen benötigt; Prior-Schätzungen und neue Informationen aus den Prüfergebnissen [8]. In dieser Studie werden die neuen Informationen aus den Inspektionsergebnissen verwendet, um die Schätzungen der Simulierten Realität zu erzeugen. Durch den Vergleich dieser beiden Informationssätze erhält man die Posteriorverteilungen der unbestimmten Parameter.

Prior-Verteilungen (kurz für A-priori-Verteilungen) drücken die Überzeugungen über die unsicheren Parameter aus, bevor die neuen Daten berücksichtigt werden. Die Prior-Verteilungen können aufgrund von theoretischen Überlegungen, Expertenmeinungen, vergangenen Erfahrungen oder in der Literatur berichteten Daten angenommen werden [2].

Feldbeobachtungen haben gezeigt, dass in Rohrverbindungen kleine Ermüdungsrisse (oft) an der Schweißnahtspitze an der Stelle des Hotspots beginnen und sich allmählich um den Schnittpunkt und durch die Rohrwand ausbreiten [9]. Für die Ermüdungsanalyse werden im Allgemeinen zwei Ansätze verwendet: der S-N-Ansatz (Wöhlerkurve) und der FM-Ansatz (Bruchmechanik). In dieser Studie wird die Analyse der Ermüdungszuverlässigkeit auf der Grundlage des FM-Ansatzes durchgeführt, da dieser Ansatz die Zunahme der Rissgröße mit der Anzahl der Ermüdungs­spannungs­zyklen in Beziehung setzt [10]. Im FM-Ansatz kann die Beziehung zwischen der Risswachstumsrate und einem Spannungsparameter mit Hilfe des Pariser Gesetzes dargestellt werden [10]:

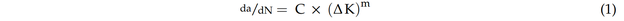
wobei a die Rissgröße darstellt, N die Anzahl der Lastwechsel ist, ΔK den Spannungsintensitätsfaktorbereich darstellt, sowie C und m die Materialparameter sind.

Der Spannungsintensitätsfaktor (SIF) ist eine Funktion der angelegten Spannung, der Größe und Form des Risses sowie der Geometrie des gerissenen Bauteils [11]. Daher ist es eine schwierige Aufgabe, eine genaue Lösung für den Spannungsintensitätsfaktor zu finden [11]. Es wurden mehrere Studien durchgeführt, um die SIFs zu erhalten. Im Allgemeinen kann der SIF auf der Grundlage empirischer Methoden [12] erhalten werden oder er kann mit Hilfe von Finite-Elemente-Methoden [13,14] berechnet werden.

Der Spannungsintensitätsbereichsfaktor kann im allgemeinen Fall wie folgt ausgedrückt werden:

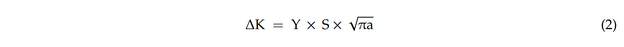
wobei Y eine Geometriefunktion und S der angelegte Spannungsbereich ist.

Durch Einsetzen von Gleichung (2) in Gleichung (1) und Integrieren von der anfänglichen Rissgröße (a₀) zur aktuellen Rissgröße (a_t) kann die Beziehung zwischen Rissgröße und Anzahl der Zyklen für die Ausbreitung eines Risses wie folgt erhalten werden:

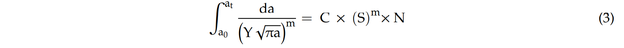
Durch Integration von Gleichung (3) kann die aktuelle Rissgröße vorhergesagt werden als:

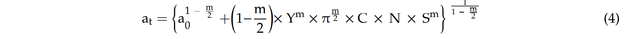
Gleichung (4) ist gültig, wenn der angelegte Spannungsbereich (S) einen konstanten Wert hat [11]. In der Realität sind die Plattformen aufgrund des Vorhandenseins mehrerer Seegangs-Zustände mehreren Belastungszuständen ausgesetzt. Daher ist der Spannungsbereich in einer rohrförmigen Verbindung nicht konstant und variiert für jeden Seegangs-Zustand. Da der Spannungsbereich in verschiedenen  Seegangs-Zuständen nicht konstant ist, kann (S)^m in Form des Erwartungswertes des Spannungsbereichs ausgedrückt werden [5]. Daher wird Gleichung (4) geschrieben als:

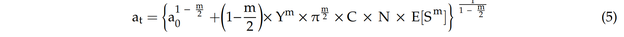
wobei E[.] der Erwartungswertoperator ist.

Um die entwickelte Methodik zu demonstrieren, wird eine Jacket-Offshore-Plattform betrachtet. Die Plattform ist ein Wohnquartier, das sich in einer Wassertiefe von 70 m befindet. Das tragende Jacket ist eine vierbeinige Stahlkonstruktion mit vier verpressten Pfählen. Die Beine sind geneigt und seitlich mit X-förmigen Streben abgestützt. Die Masse der Oberseite wird auf 2200 Tonnen geschätzt.

Ein dreidimensionales Finite-Elemente-Modell der Plattform wird mit der Software SESAM [15] erstellt und eine globale spektrale Ermüdungsanalyse mit charakteristischen Variablen durchgeführt. Die Umgebungsbelastung wird in Form eines Satzes von stationären Seemodelliert, wobei jeder Seezustand durch eine signifikante Wellenhöhe, eine mittlere Periode des Nulldurchgangs, die Wellenrichtung und ein Wellenspektrum charakterisiert ist.

Die Software ist in der Lage, den quadratischen Mittelwert der Spannung (σ) für jeden Seegang zu berechnen. Bei der Anwendung auf die Offshore-Jacket-Strukturen wird die Wellenbelastung als schmalbandiger Gauß-Prozess betrachtet [5]. Für einen schmalbandigen Gauß-Prozess sind die Spannungsbereiche Rayleigh-verteilt. Der Mittelwert des Ermüdungsspannungsbereiches für den i-ten Seegang ist gleich [16]:

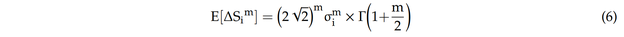
Dabei ist Γ die Gamma-Funktion und σi der quadratische Mittelwert der Spannung für den i-ten Seegang. Der Gesamterwartungswert des Spannungsbereichs kann wie folgt berechnet werden [16]:

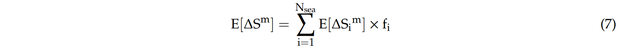
wobei N_sea die Anzahl der Seezustände ist und f_i die Wahrscheinlichkeit des Auftretens jedes Seezustands ist. Sie ist der Anteil der Zeit, in der der i-te Seegang beobachtet wird.

Außerdem kann für einen schmalbandigen Gauß-Prozess die Gesamtzahl der Spannungszyklen wie folgt abgeschätzt werden [11]:

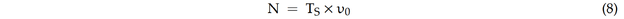
wobei T_S die Zeit in Jahren und υ₀ die Häufigkeit der Nulldurchgänge des Spannungsprozesses ist. Der Einfachheit halber wird die mittlere Rate der Nulldurchgänge mit υ₀ = 5 × 10⁶ pro Jahr angenommen.

Durch Einsetzen von Gleichung (8) in Gleichung (5) kann die aktuelle Rissgröße vorhergesagt werden als:

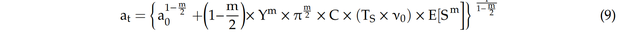
Gleichung (9) zeigt, dass die vorhergesagte Rissgröße (a_t) eine Funktion mehrerer Parameter ist, wie z. B. der Anfangsrissgröße (a0), der Materialeigenschaften (C), der Geometriefunktion (Y) und des Spannungsbereichs (E[S^m]).

Um die in dieser Studie beschriebene Methodik anzuwenden, wird eine Beispielverbindung betrachtet. Bei der betrachteten Verbindung handelt es sich um ein rohrförmiges Y-Gelenk, bei dem der Sehnen- und Strebendurchmesser 914 bzw. 660 mm beträgt. Außerdem betragen die Gurt- und Strebenstärken 25,4 bzw. 19,2 mm. Nachdem der quadratische Mittelwert der Spannung für jeden Seegang ermittelt wurde, wird der erwartete Wert des Spannungsbereichs für das betrachtete Gelenk auf 180 MPa berechnet.

Bei der Vorhersage der Ermüdungslebensdauer in Rohrverbindungen gibt es mehrere Unsicherheiten, wie z. B. die Variation des Spannungsbereichs, der Umgebungs­para­meter und der Spannungsintensitätsfaktoren. Die folgenden Unsicherheiten werden in dieser Arbeit berücksichtigt:

(1) Anfängliche Rissgröße: Die Anfangsrissgröße ist eine wichtige Variable, die die Ermüdungslebensdauer einer rohrförmigen Verbindung beeinflusst. Die Anfangsrissgröße ist kein bekannter Parameter und daher ist die Modellierung dieses Parameters mit Unsicherheiten verbunden [5].

(2) Risswachstumsparameter: Ermüdungsversuche zeigen eine beträchtliche Streuung in den erhaltenen Ermüdungskapazitäten, die auf die Materialeigenschaften zurückzuführen ist. Es besteht immer eine Unsicherheit bei der Definition von sinnvollen Verteilungen für die Materialparameter, die auf den verfügbaren Laborversuchsergebnissen basieren [5].

(3) Geometriefunktion: In der Literatur sind einige empirische Ausdrücke für die Geometriefunktion für einfache Schweißverbindungen angegeben [12]. Es gibt jedoch keine analytische Lösung für die Geometriefunktion für komplexe Geometrien wie Rohrverbindungen und die experimentellen Daten zeigen eine Streuung für die Geometriefunktion [9].

(4) Spannungsbereich: Das Spannungsbereichsspektrum wird durch die Annahme von Beziehungen zwischen Wellenhöhe und Wellenspannungsspektren erhalten. Außerdem sind bei der globalen Ermüdungsanalyse mehrere Unsicherheiten beteiligt (z. B. Umgebungsparameter, hydrodynamische Belastungen usw.) [17]. Daher wird der berechnete Spannungsbereich für die betrachtete Rohrverbindung als unsicherer Parameter angenommen.

Die berücksichtigten Unsicherheiten und ihre Verteilungen, die an der Berechnung der Ermüdungsschädigung beteiligt sind, sind in Tabelle 1 dargestellt.

Tabelle 1: Statistik der Unsicherheiten (zum Vergrößern bitte anklicken)

Nach der Vorhersage der Rissgröße basierend auf dem FM-Ansatz kann die Versagenswahrscheinlichkeit mit Hilfe einer Grenzzustandsfunktion berechnet werden. Die Grenzzustandsfunktion stellt die Grenze zwischen dem sicheren und unsicheren Verhalten eines Systems oder einer Komponente dar [19].

Verschiedene Kriterien wie das Rissgrößenkriterium und das Kriterium der äquivalenten Ermüdungsfestigkeit wurden vorgeschlagen, um den Ermüdungsgrenzzustand von Rohrverbindungen mit Rissen zu beschreiben [20]. Beim Rissgrößenkriterium tritt das Versagen ein, sobald die Rissausbreitung größer als ein kritischer Wert ist, während beim äquivalenten Dauerfestigkeitskriterium das Versagen eintritt, wenn der Spannungsintensitätsfaktor in der Rissspitze größer als die Bruchzähigkeit ist. In dieser Studie wird die Rissgröße als ein Versagenskriterium für die Zuverlässigkeits­berechnungen behandelt. Daher wird die Ermüdungs­grenz­zustands­funktion wie folgt beschrieben [20]:

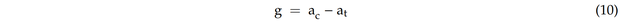
wobei a_c die kritische Rissgröße ist. Die kritische Rissgröße kann basierend auf Kriterien der Gebrauchstauglichkeit (z. B. Riss durch die Dicke oder wirtschaftliche Reparaturgrenzen) oder Kriterien des endgültigen Zusammenbruchs (z. B. instabiler Bruch) definiert werden [5]. Die kritische Rissgröße kann als die Wanddicke für die Zuverlässigkeitsanalyse angenommen werden [5,20].

In dieser Studie wird die Monte-Carlo-Simulation verwendet, um die Ausfallwahrscheinlichkeit zu erhalten. Um die Zuverlässigkeit mittels Monte-Carlo-Simulation zu erhalten, werden die folgenden Schritte berücksichtigt [21]:

1. Eine große Anzahl von Stichproben für jeden unsicheren Parameter wird basierend auf der in Tabelle 1 angegebenen Verteilung erzeugt;
      
2. Die Grenzzustandsfunktion (Gleichung (10)) wird für jeden Satz von Stichproben (Versuche) ausgewertet;
      
3. Die Ausfallwahrscheinlichkeit wird geschätzt als:

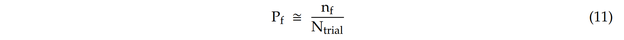
wobei n_f die Anzahl der Versuche ist, bei denen die Grenzzustandsfunktion kleiner oder gleich Null ist (d. h. die Rissgröße übersteigt die kritische Größe) und Ntrial die Gesamtzahl der Versuche ist.

Eines der Ziele dieser Studie ist es, die Rissgrößenverteilung zu aktualisieren, wenn neue Inspektionsdaten verfügbar sind. Der erste Schritt der Aktualisierung besteht darin, eine geeignete Vorverteilung der Rissgröße zu wählen. Die Prior-Rissgrößenverteilung kann aufgrund von theoretischen Überlegungen, Expertenmeinungen, früheren Erfahrungen oder Daten aus der Literatur angenommen werden [2]. Die vorgeschlagene Rissgrößenverteilung basiert jedoch auf begrenzten experimentellen Versuchen.

In dieser Studie wird eine Stichprobenmethode vorgeschlagen, um die Rissgrößenverteilung zu erhalten. Zu diesem Zweck wird eine große Anzahl von Stichproben, N^p, erzeugt, indem Zufallszahlen verwendet werden, die aus den Verteilungen der unsicheren Parameter gewonnen werden.

Für jeden Satz von generierten Stichproben wird die Prior-Rissgröße mit Hilfe von Gleichung (9) berechnet. Zum Beispiel wird für die k-te Probe die Prior-Rissgröße (a^p_k) wie folgt berechnet:

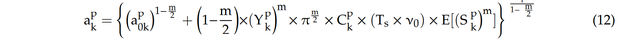
mit k = 1, 2, ..., N^p. Hier wird die Anzahl der Stichproben mit N^p = 10⁵ berücksichtigt. Ein großer Wert der Stichproben verbessert die Wahrscheinlichkeit, dass alle relevanten Kombinationen dieser Zufallsvariablen enthalten sind. Es wird ein Python-Code geschrieben, um die Rissgrößenverteilung zu erhalten, indem Zufallsstichproben für jeden unsicheren Parameter erzeugt werden [22].

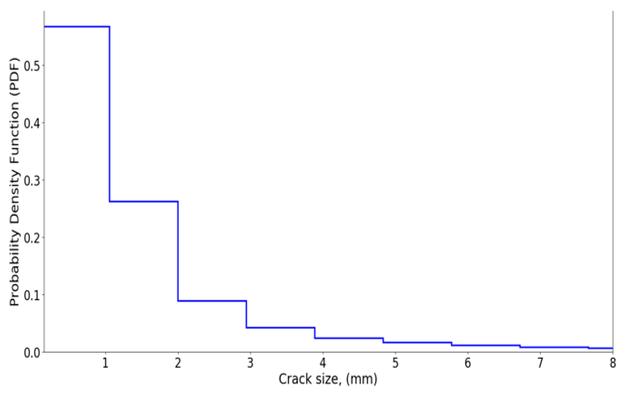
Bild 1 zeigt das normalisierte Histogramm der vorhergesagten Rissgrößen nach fünf Jahren (Ts = 5) basierend auf den generierten Stichproben, die als Prioritätsverteilung für die Rissgröße verwendet wird.

Bild 1: Ermittlung der Rissgrößenverteilung mithilfe der Probenahmemethode

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

In einer Schweißverbindung, wie z. B. einer Rohrverbindung in den Offshore-Plattformen, sind in der Regel mehrere Ermüdungsrisse vorhanden. Nicht alle dieser vorhandenen Risse können detektiert werden. Die Wahrscheinlichkeit der Entdeckung eines Risses hängt von der Auflösung der Prüftechnik ab. Es gibt eine Vielzahl von NDT-Techniken zum Auffinden von Rissen [23]. Die Erkennungswahrscheinlichkeit (Probability of Detection, POD), variiert mit der Rissgröße und der angewandten Prüftechnik. Die Erkennungswahrscheinlichkeit eines Risses ist in der Regel gegeben durch [23]:

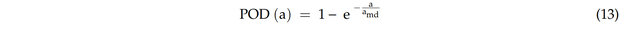
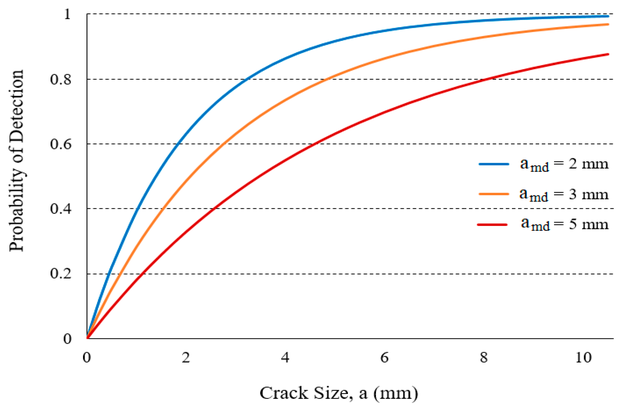
wobei amd, die mittlere detektierbare Größe ist und von der Auflösung der Prüftechnik abhängt [23]. Bild 2 zeigt die POD-Kurven für verschiedene mittlere detektierbare Größen.

Bild 2: Kurven der Wahrscheinlichkeit der Erkennung (Probability of Detection, POD) für verschiedene mittlere nachweisbare Größen

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Im Allgemeinen ist amd ein unsicherer Wert, daher wird in dieser Studie der Prior-Schätzung der mittleren nachweisbaren Größe eine Lognormalverteilung (LN) zugewiesen als: 

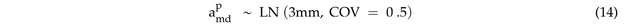
Hier wird eine große COV für amd berücksichtigt, um den Prior so nicht-informativ wie möglich zu haben. Nicht-informative Priors sollen die Daten (Beobachtungen) die Posterior-Verteilung dominieren lassen; sie enthalten also wenig substanzielle Informationen über den interessierenden Parameter [24]. Um herauszufinden, welcher Prior-Riss erkannt werden kann, werden N^p Zufallswerte von a^pmd basierend auf der definierten Verteilung ausgewählt.

In den vorherigen Abschnitten wurden N^p-Simulationen für die Rissgröße (a^p) und auch für die mittlere detektierbare Größe (a^pmd) durchgeführt. Daher ist für jede Rissgröße ein entsprechender Wert für die mittlere erkennbare Größe verfügbar. Im Allgemeinen können winzige Risse mit keiner ZfP-Technik erkannt werden. Es sollte ein Kriterium definiert werden, das zeigt, welche Prior-Rissgröße (mit der entsprechenden a^pmd) detektierbar ist und welche übersehen wird. Das vorgeschlagene Kriterium wird im Folgenden beschrieben:

(1) Für jeden Satz von (a^p, a^p_md)j, mit j = 1, 2, ..., N^p; (PODN^p)j wird mit Gleichung (13) berechnet

(2) 10⁵ Zufallszahlen werden aus einer Gleichverteilung zwischen [0, 1] ausgewählt, d. h.,:
   

(3) (Chance^p)_j = Zufallszahl, mit j = 1, 2, ..., 10⁵

(4) Eine Prior-Rissgröße wird als erkannte Rissgröße (a^det_p)j angenommen, wenn:

              a. (Chance^p)_j ≤ (PODe^p)_j mit j = 1, 2,..., 10⁵

     
(5) Andernfalls wird die simulierte Prior-Rissgröße als verpasst angenommen ("the simulated prior crack size is assumed as a missed one").

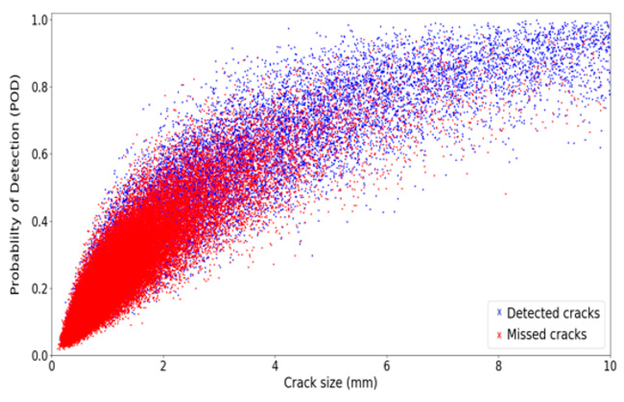
Bild 3 zeigt die erkannten und verpassten Risse basierend auf dem definierten Kriterium. Wie die Abbildung zeigt, handelt es sich bei der Mehrzahl der verpassten Risse um winzige Defekte, die mit ZfP-Techniken kaum zu erkennen sind.

Bild 3: Erkannte/verpasste Risse, die durch die Implementierung des Erkennungskriteriums erhalten wurden

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Es wurde gezeigt, dass die vorhergesagte Rissgröße in einer bestimmten Verbindung eine Funktion der Anfangsrissgröße, des Risswachstumsparameters, des Spannungsbereichs und der Geometriefunktion ist. Die angenommenen Verteilungen dieser Eingangsgrößen haben einen großen Einfluss auf die Rissgrößenverteilung [5,25]. Daher ist es entscheidend, die glaubwürdigsten Verteilungen für diese Parameter zu wählen.

Die Genauigkeit der Ergebnisse der Zuverlässigkeitsanalyse ist abhängig von den angenommenen Verteilungen [25]. Es wurde erwähnt, dass die verschiedenen empfohlenen Praktiken verschiedene Prioritätsverteilungen für die unsicheren Parameter einführen. Diese Verteilungen werden jedoch auf der Basis von experimentellen Tests gewonnen. Daher sind sie nicht repräsentativ für die realen Verteilungen. Zum Beispiel wird der Risswachstumsparameter normalerweise durch die Anpassung von Ermüdungstestdaten geschätzt, die unter kontrollierten Laborbedingungen gemessen wurden, die sich von den tatsächlichen Bedingungen auf Offshore-Plattformen unterscheiden [2].

Da die realen Verteilungen für diese unsicheren Parameter unbekannt sind, wird in dieser Studie ein Ansatz verwendet, der als Ansatz der Simulierte-Realitäts-Verteilungen bezeichnet wird, um die realen Verteilungen zu erhalten. Dieser Ansatz basiert auf dem Konzept der äquivalenten Anfangsfehlergröße.

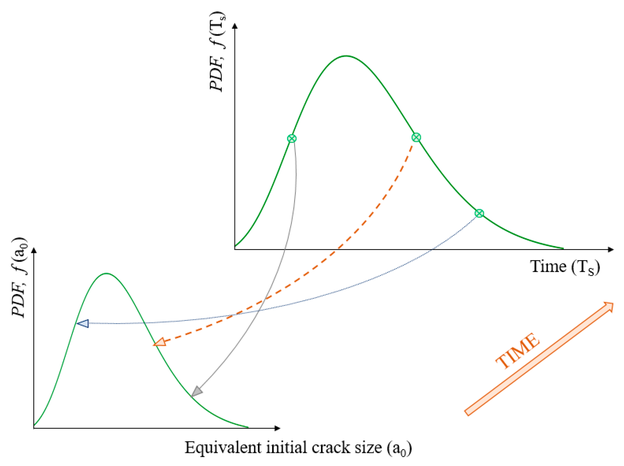
3.1 Konzept der äquivalenten Anfangsrissgröße

Bei der Zuverlässigkeitsanalyse von Flugzeugstrukturen spielt die anfängliche Rissgrößenverteilung eine entscheidende Rolle [26]. Um die anfängliche Rissgrößenverteilung zu erhalten, führten Gray und Rudd [26] das Konzept der äquivalenten anfänglichen Fehlergröße (Equivalent Initial Flaw Size, EIFS) ein. Dieses Konzept wurde von Yang und Manning [27] für die probabilistische Risikoanalyse von Flugzeugen entwickelt.

Die EIFS-Verteilung wird normalerweise durch Rückextrapolation der beobachteten Rissgröße auf die entsprechende Größe zum Zeitpunkt Null erhalten. Dies beinhaltet die Anpassung eines Risswachstumsmodells an die Rissgröße. Daher ist das EIFS eine künstliche Rissgröße [26] und für eine beobachtete Rissgröße ist das EIFS nicht eindeutig, d. h. für die gleichen beobachteten Rissgrößen können unterschiedliche EIFS-Werte durch die Verwendung unterschiedlicher Risswachstumsmodelle erreicht werden [26]. Trotz dieser Unzulänglichkeit wurde das Konzept des EIFS zur Quantifizierung der anfänglichen Rissgrößenverteilungen verwendet, da es mit dem Risswachstum konsistent ist, um die Rissgröße zu einem bestimmten Zeitpunkt zu berechnen [26].

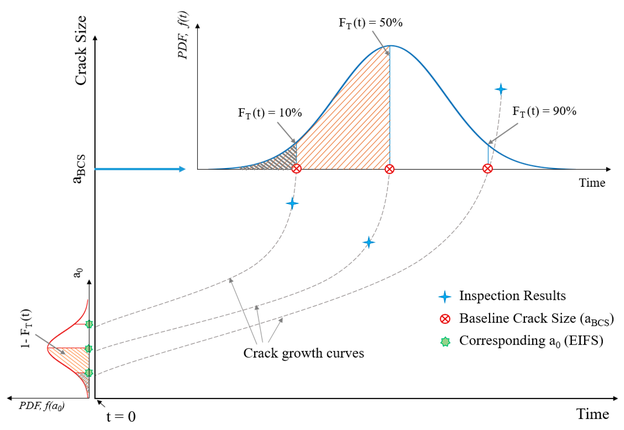
Für einen gegebenen Satz von Rissgrößen (für eine bestimmte Verbindung zu verschiedenen Zeitpunkten) können die äquivalenten anfänglichen Rissgrößenverteilungen (EIFS) mit den entsprechenden Risswachstumskurven wie folgt erhalten werden:

(1) Eine bestimmte Rissgröße wird als Basisrissgröße (baseline crack size, a_BCS) gewählt

(2) Für einen gegebenen Satz von Rissgrößen werden die Rissgrößen, die größer als die Basisrissgröße sind, anhand der Risswachstumskurve regressiert. Außerdem werden die Rissgrößen, die kleiner als die Basisrissgröße sind, mit Hilfe der Risswachstumskurve gewachsen.

(3) Dem Zeitpunkt, zu dem die Risse die Größe von a_BCS erreichen, wird eine Wahrscheinlichkeitsdichtefunktion (PDF) zugeordnet.

(4) Die Zeitverteilung der Basisrissgröße wird mit einer kumulativen Wahrscheinlichkeit von (1 - F_T(t)) auf eine Anfangsrissgröße übertragen.

(5) Schließlich erhält man eine geeignete Verteilung für die äquivalente Anfangsrissgröße (EIFS).

Bild 4 veranschaulicht die Methode zur Gewinnung der EIFS-Verteilung.

Bild 4: Ermitteln der äquivalenten Anfangsfehlergrößenverteilung (EIFS)

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Die EIFS-Verteilung wird durch Regression der beobachteten Rissgrößen aus Inspektionsergebnissen zurück auf den Beginn der Ermüdungslebensdauer bestimmt [27]. Um eine geeignete Verteilung zu erhalten, wird jedoch eine ausreichende Anzahl von Datenpunkten benötigt, wobei die Inspektionsdaten sehr begrenzt und teuer zu beschaffen sein können. Daher hängt die Qualität der EIFS-Verteilung von der Anzahl der verfügbaren Inspektionsergebnisse ab [27].

In der Literatur wurde der EIFS-Ansatz betrachtet, um die anfängliche Rissgrößenverteilung von Flugzeugen zu erhalten. Für die Zuverlässigkeitsanalyse von Offshore-Plattformen hängt die Verteilung der Rissgröße zu einem bestimmten Zeitpunkt jedoch von mehreren unsicheren Parametern ab, wie in Gleichung (9) dargestellt. Daher wird in dieser Studie der EIFS-Ansatz erweitert, um die äquivalente Verteilung für alle unsicheren Parameter, die die Rissgröße in einer rohrförmigen Verbindung beeinflussen, zu erhalten.

3.2. Simulierte-Realitäts-Verteilungen für unsichere Parameter

Die Ergebnisse der Ermüdungsprüfung enthalten nur Informationen über die Rissgrößen. Da die Inspektion keine expliziten Informationen über die anderen unsicheren Parameter liefern kann, sind die Verteilungen dieser Parameter unbekannt. Zu diesem Zweck wird das Konzept der Ersatzverteilungen verwendet, um die Verteilung dieser Parameter in der Simulierten Realität vorherzusagen.

Um den betrachteten Ansatz zu demonstrieren, wird angenommen, dass für die betrachtete Rohrverbindung fünf Inspektionsergebnisse in verschiedenen Jahren zur Verfügung stehen. Tabelle 2 zeigt die angenommenen Inspektionsergebnisse.

Tabelle 2: Angenommene Inspektionsergebnisse für die betrachtete rohrförmige Verbindung (zum Vergrößern bitte anklicken)

Um die Simulierte-Realitäts-Verteilung für die Anfangsrissgröße zu erhalten, wird die Basisrissgröße mit a_BCS= 4 mm gewählt. Für die gegebenen Rissgrößen in Tabelle 2 werden die Rissgrößen, die größer als 4 mm sind, regressiert und die Rissgrößen, die kleiner als 4 mm sind, werden mithilfe der Risswachstumskurve gewachsen. Tabelle 3 zeigt die Zeit bis zum Erreichen von 4 mm für jeden Riss.

Tabelle 3: Risswachstum/Regression (zum Vergrößern bitte anklicken)   

Der Mittelwert und die Standardabweichung der letzten Spalte in Tabelle 3 werden gleich 4,9 mm und 1,87 mm berechnet. Daher wird die folgende Lognormalverteilung für die Verteilung der Zeit, in der der Riss die Grundrissgröße erreicht, berücksichtigt:   

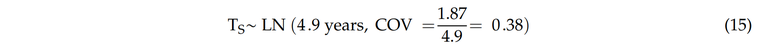
Um die Simulierte-Realitäts-Verteilung für die Anfangsrissgröße zu erhalten, werden die Mittelwerte des Risswachstumsparameters, des Spannungsbereichs und der Geometriefunktion ausgewählt. Eine große Anzahl von Zufallsstichproben wird für die Zeit (TS) basierend auf Gleichung (15) generiert und für jede Stichprobe wird die entsprechende anfängliche Rissgröße durch Verwendung von Gleichung (9) erhalten.

Bild 5 zeigt schematisch, wie die äquivalente anfängliche Rissgrößenverteilung durch Verwendung des vorgeschlagenen Ansatzes für drei zufällig generierte Zeiten erhalten wird.

Bild 5: Ermitteln der äquivalenten Anfangsrissgrößenverteilung

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

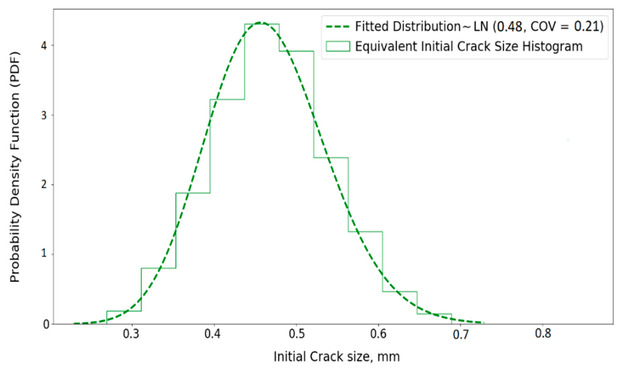
Nachdem die Anfangsrissgröße für jede Probe ermittelt wurde, wird die beste Verteilung für das Histogramm der äquivalenten Anfangsrissgröße angepasst. Bild 6 zeigt die erhaltene äquivalente Anfangsrissgrößenverteilung für die betrachtete Rohrverbindung.

Bild 6: Histogramm der äquivalenten Anfangsrissgröße und die angepasste Verteilung

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

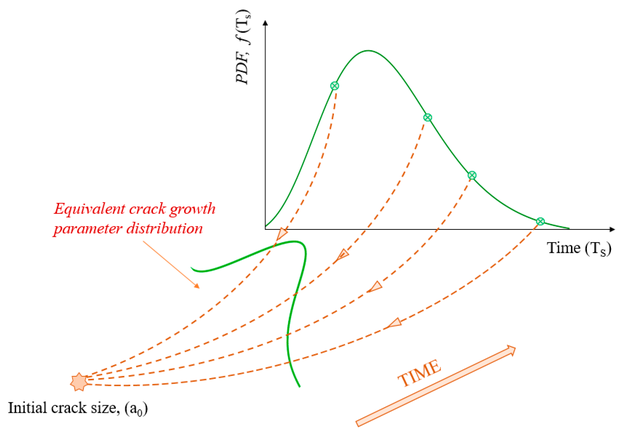
Der gleiche Ansatz wird verwendet, um die äquivalente Verteilung für den Risswachstumsparameter (C) herzuleiten. Auch hier wird eine große Anzahl von zufällig erzeugten Stichproben für die Zeit (TS) basierend auf der Lognormalverteilung ausgewählt. Um die Simulierte-Realitäts-Verteilung für den Risswachstumsparameter zu erhalten, werden die Mittelwerte der Anfangsrissgröße, des Spannungsbereichs und der Geometriefunktion ausgewählt. Bild 7 zeigt, wie die äquivalente Risswachstums-Parameter-Verteilung durch die Verwendung des vorgeschlagenen Ansatzes erhalten wird.

Bild 7: Ermittlung der äquivalenten Risswachstums­parameter­verteilung

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

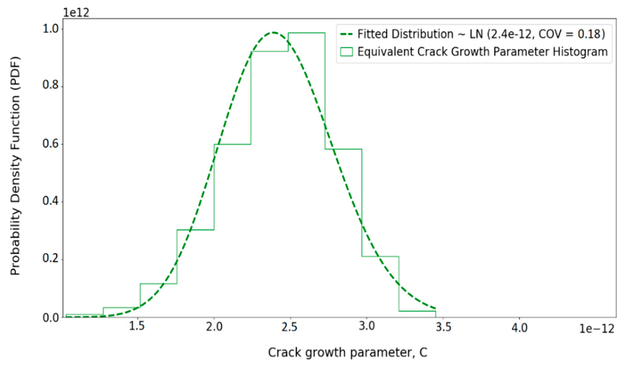
Nachdem der Risswachstumsparameterwert für jede Probe ermittelt wurde, wird die beste Verteilung für die äquivalente Risswachstumsparameterverteilung angepasst. Bild 8 zeigt die erhaltene Verteilung der äquivalenten Risswachstumsparameter für die betrachtete Rohrverbindung.

Bild 8: Histogramm der äquivalenten Risswachstumsparameter und die angepasste Verteilung

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

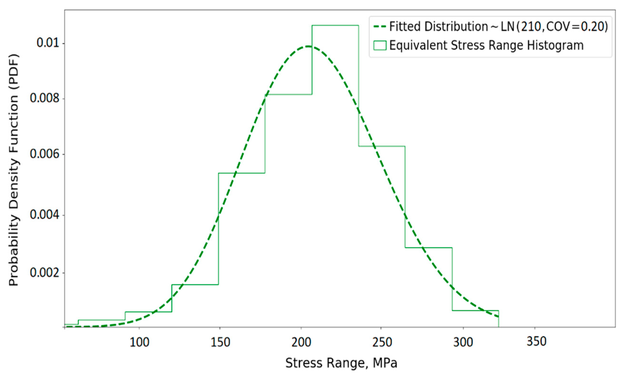
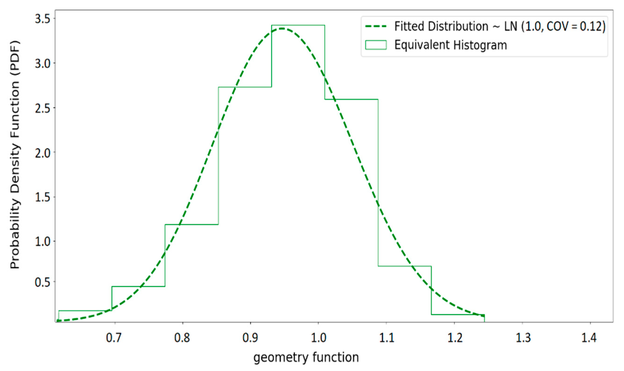
Ein ähnlicher Ansatz wird verwendet, um die äquivalente Verteilung für den Spannungsbereich und die Geometriefunktion zu erhalten. Bild 9 und Bild 10 zeigen die erhaltenen Ersatzverteilungen für den Spannungsbereich bzw. die Geometriefunktion.

Bild 9: Histogramm des Vergleichsspannungsbereichs und die angepasste Verteilung

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Bild 10: Histogramm der äquivalenten Geometriefunktion und die angepasste Verteilung

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Tabelle 4 fasst die erhaltenen Ersatzverteilungen für die unsicheren Parameter zusammen, die als die realen Verteilungen angenommen werden. Da diese Verteilungen auf der Basis von Stichprobenverfahren erzielt werden, werden sie in dieser Arbeit als Simulierte-Realitäts-Verteilungen bezeichnet.

Tabelle 4. Simulierte-Realitäts-Verteilungen für die unsicheren Parameter (zum Vergrößern bitte anklicken)   

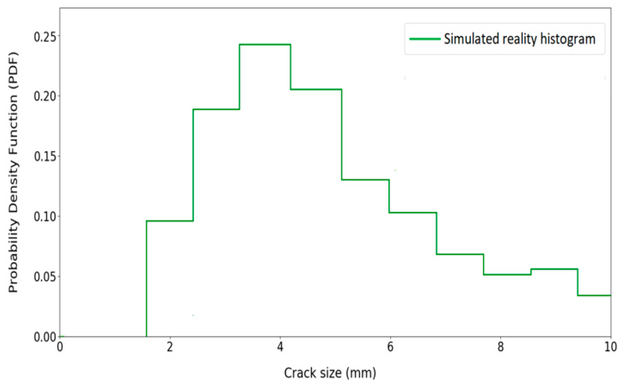
Nachdem die Simulierte-Realitäts-Verteilungen für die Eingangsgrößen erhalten wurden, kann die Simulierte-Realitäts-Verteilung für die Rissgröße ermittelt werden. Auch hier wird ein Stichprobenverfahren verwendet, um die Simulierte-Realitäts-Verteilung für die Rissgrößen nach fünf Jahren zu erhalten. Zu diesem Zweck werden N^r = 1000 Zufallszahlen für jede Eingangsvariable auf der Grundlage ihrer in Tabelle 4 dargestellten Verteilungen erzeugt. Für jeden Satz von Stichproben (z. B. für den k-ten Stichprobensatz: a^r_0k, C^r_k, S^r_k und Y^r_k) wird die Rissgröße (a^r_k) basierend auf Gleichung (9) berechnet. Bild 11 zeigt das normalisierte Histogramm der Simulierte-Realitäts-Rissgrößen nach fünf Jahren, das als Simulierte-Realitäts-Verteilung für die Rissgröße verwendet wird. 

Bild 11: Simulierte-Realitäts-Verteilung für die Rissgröße

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Es wird darauf hingewiesen, dass in der Praxis aufgrund der hohen Kosten für die Inspektion nur wenige Inspektionsergebnisse für jede Rohrverbindung zur Verfügung stehen. In der vorgeschlagenen Stichprobenmethode wird statt einiger weniger Inspektionsergebnisse eine große Anzahl künstlicher Rissgrößen verwendet, die auf der Grundlage von Inspektionsergebnissen erzeugt werden. Diese generierten Risse können zur Verbesserung der Verteilung der unsicheren Parameter verwendet werden.

Es wurde erwähnt, dass die Wahrscheinlichkeit der Erkennung eines Risses von der Auflösung der Prüftechnik abhängt. Hier wird eine Lognormalverteilung mit einem Mittelwert von 2 mm und einem Variationskoeffizienten (COV) von 0,2 für die Simulierte-Realitäts-Verteilung der mittleren erkennbaren Größe als berücksichtigt:

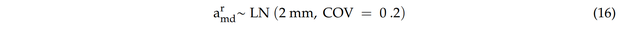
Um herauszufinden, welcher Simulierte-Realitäts-Riss erkannt werden kann, werden N^r zufällige Werte von a^r_md basierend auf der definierten Lognormalverteilung in Gleichung (16) ausgewählt.

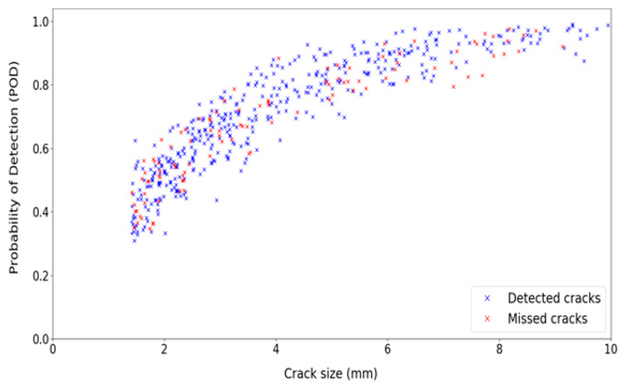
In den vorherigen Abschnitten wurden 1000 Rissgrößen (a^r) und 1000 mittlere detektierbare Größen (a^r_md) erzeugt. Daher ist für jede Rissgröße ein entsprechender Wert der mittleren erkennbaren Größe verfügbar. Einige der bei der Stichprobenmethode erzeugten Risse sind winzig. Daher können sie nicht mit Hilfe von ZfP-Techniken erkannt werden. Bei diesem Ansatz sollen diejenigen Risse verwendet werden, die erkannt werden können.

Das gleiche Kriterium wie in Abschnitt 2.7 wird verwendet, um zu entscheiden, welche Rissgröße (mit dem entsprechenden a^r_md) detektierbar ist und welche übersehen wird. Bild 12 zeigt sowohl erkannte als auch verpasste Risse.

Bild 12: Erkannte/verpasste Risse, die durch die Umsetzung des Erkennungskriteriums erhalten werden

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

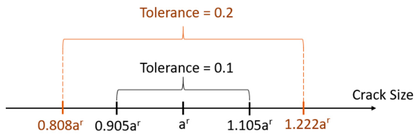
Nun gibt es zwei Sätze von Rissen: erkannte Prior-Risse und erkannte Simulierte-Realitäts-Risse. Um die Posterior-Verteilung zu erhalten, wird jeder erkannte Prior-Riss mit den Simulierte-Realitäts-Rissen verglichen, um festzustellen, ob der erkannte Prior-Riss mit der Realität kompatibel ist. Wenn der Prior-Riss "nahe" am Simulierte-Realitäts-Riss liegt, wird dieser Prior-Riss als kompatible Simulation angenommen. Der Prior-Riss wird als kompatible Simulation betrachtet, wenn die folgende Bedingung erfüllt ist: Erkannte/verpasste Risse, die durch die Umsetzung des Erkennungskriteriums erhalten werden.   

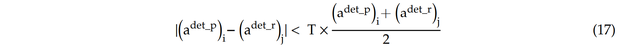
mit

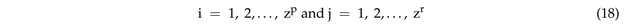
wobei A^det_p und a^det_r die erkannte Prior-Rissgröße bzw. die erkannte Simulierte-Realitäts-Rissgröße darstellen. Die Parameter zp und zr stehen für die Anzahl der erkannten Prior-Risse bzw. der Simulierte-Realitäts-Risse.

Um das Wort "nah" zu quantifizieren, wird der Parameter T für die akzeptable Toleranz betrachtet. Wenn ein kleiner Wert für die Toleranz gewählt wird, sollte die Differenz zwischen dem Prior-Riss und dem Simulierte-Realitäts-Riss klein sein. Auf der anderen Seite erlaubt ein großer Wert für die Toleranz einen größeren Unterschied zwischen dem Prior-Riss und dem Simulierte-Realitäts-Riss . Abbildung 13 zeigt den akzeptablen Bereich für einen Prior-Riss für zwei verschiedene Toleranzen. Um die Methodik zu demonstrieren, wird in dieser Studie der Parameter T gleich 0,2 angenommen.

Bild 13: Die akzeptablen Bereiche für die vorherigen Risse

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Basierend auf der Kompatibilitätsdefinition in Gleichung (17) stimmen viele vorherige Simulationen möglicherweise mit keinem realen Fall überein. Einige Prior-Simulationen können jedoch mit mehreren realen Fällen übereinstimmen. Unter Verwendung von Gleichung (17) werden die Prior-Risse in zwei Kategorien aufgeteilt: kompatible Prioren und inkompatible Prioren. Um die Posterior-Verteilung zu erhalten, werden die inkompatiblen Prior-Simulationen entfernt und die kompatiblen Prior-Simulationen werden als die Posterior-Risse betrachtet. Durch die Implementierung dieses Ansatzes werden die neuen Daten (die simulierte Realitätsrisse sind) verwendet, um die Prior-Risse zu verbessern und die Posterior-Verteilung der Rissgrößen zu erhalten.

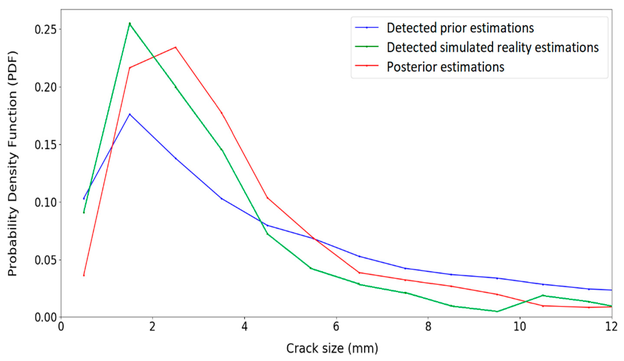
Bild 14 zeigt die Posterior-Verteilung der Rissgrößen, die auf der Grundlage der kompatiblen Prioren erhalten werden. Obwohl sowohl detektierte Prior-Risse als auch detektierte Risse der Simulierten Realität die Form der Posterior-Verteilung beeinflussen, ist zu beobachten, dass sich die Posterior-Verteilung in Richtung der Verteilung der Simulierten Realität bewegt hat.

Bild 14: Rissgrößenverteilungen vor und nach dem Aktualisieren

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Es wird auch beobachtet, dass die Posterior-Verteilung schmaler ist als die Prior-Verteilung. Daher ist die Unsicherheit der Posterior-Verteilung für die Rissgröße im Vergleich zur Prior-Verteilung geringer. Tatsächlich wird durch die Implementierung der Prüfergebnisse die Posterior-Verteilung für die Rissgröße weniger unsicher als das Vorwissen.

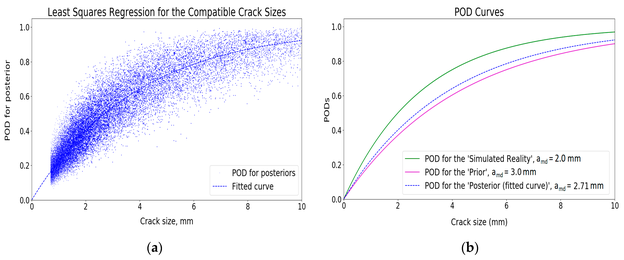
Durch Entfernen der inkompatiblen Prior-Risse kann die posteriore POD-Kurve erreicht werden. Abbildung 15a zeigt kompatible vorherige Simulationsergebnisse und die angepasste Verteilung. Wie aus Abbildung 15b ersichtlich ist, hat sich die posteriore POD-Kurve in Richtung der Simulierte-Realitäts-Daten bewegt.

Bild 15: Aktualisierung der POD-Kurve basierend auf den kompatiblen Simulationen: (a) Kompatible vorherige Simulationsergebnisse; (b) Angepasste Entdeckungs­wahr­schein­lichkeits­kurve  (POD-Kurve)

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Wenn ein bestimmter erkannter vorheriger Riss, adet_pj, inkompatibel ist, bedeutet dies, dass die Kombination der entsprechenden Eingabevariablen (ap0j, Cpj, Ypj und Spj) keine akzeptable vorherige Rissgröße erzeugt. Daher werden diese Werte (ap0j, Cpj, Ypj und Spj) aus dem Anfangssatz der vorherigen Simulationen entfernt. Andererseits, wenn ein simulierter Prior-Riss eine kompatible Rissgröße mit der Simulierten Realität ist ("if a simulated prior crack is a compatible crack size with the simulated reality"), sind die entsprechenden Eingabevariablen geeignete Werte und sie werden beibehalten, um sie für die posterioren Verteilungen zu verwenden.

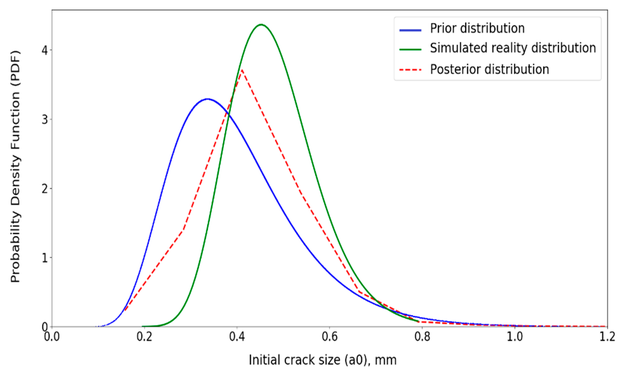
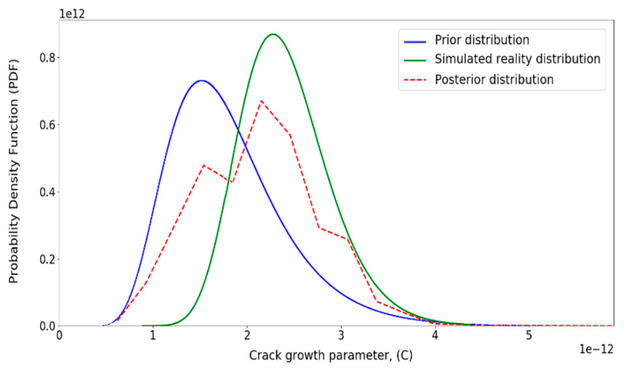
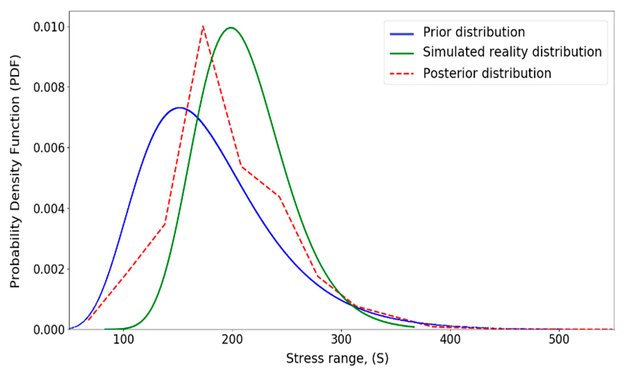
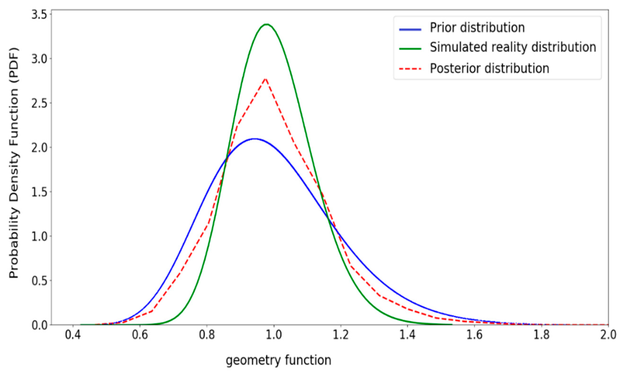
Bild 16, Bild 17, Bild 18 und Bild 19 zeigen die Posteriorverteilungen für die unsicheren Eingangsvariablen. Ähnlich wie in Abbildung 14 haben sich die Posteriorverteilungen der unsicheren Parameter in Richtung der Simulierte-Realitäts-Verteilung bewegt. Zum Beispiel in Bild 17, wenn der Risswachstumsparameter etwa 10^-12 ist, ist die Posterior-Verteilung aufsteigend und die Prior-Verteilung absteigend. Die Abbildung veranschaulicht, dass die Posterior-Verteilung dazu tendiert, sich in Richtung der Simulierte-Realitäts-Verteilung zu verschieben.

Bild 16: Aktualisierte Verteilung für die Anfangsrissgröße (a₀)

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Bild 17: Aktualisierte Verteilung für Risswachstumsparameter (C)

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Bild 18: Aktualisierte Verteilung für Spannungsbereich (S)

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Bild 19: Aktualisierte Verteilung für Geometriefunktion (Y)

© H. Khalili, S. Oterkus, N. Barltrop und U. Bharadwaj, CC BY 4.0

Außerdem ist in diesen Bildern der wahrscheinlichste Betrag der Zufallsvariablen (Moduswert) in Richtung des Moduswertes der Simulierte-Realitäts-Verteilungen verschoben. Es ist erwähnenswert, dass die Form der posterioren Verteilung sowohl von den prioren als auch von den Simulierte-Realitäts-Verteilungen  beeinflusst wird.

Die aktualisierten Verteilungen können als die prioren Verteilungen für den nächsten Aktualisierungsprozess verwendet werden, wenn neue Prüfergebnisse verfügbar sind. Daher können für den nächsten Aktualisierungsprozess anstelle der Verwendung von verallgemeinerten Verteilungen, die von den empfohlenen Verfahren bereitgestellt werden, realistischere Verteilungen als Prior-Verteilungen ausgewählt werden.

In Bild 14 ist zu erkennen, dass die Unsicherheit der posterioren Rissgrößenverteilung abnimmt. Es ist jedoch zu beobachten, dass die Unsicherheit der posterioren Verteilungen der anderen Parameter aufgrund der beteiligten Unsicherheiten sowohl in den prioren als auch in den simulierten Realitätsverteilungen zunimmt. Der Grund dafür ist, dass die Prüfergebnisse nur die Information über die Rissgröße enthalten und keine expliziten Informationen über die anderen Parameter liefern.

Obwohl die Unsicherheit der posterioren Verteilungen der Eingangsvariablen zunimmt, werden die prioren Verteilungen der Eingangsvariablen basierend auf der realen Situation der betrachteten Rohrverbindung modifiziert. Es wurde erwähnt, dass die prioren Verteilungen auf experimentellen Tests basieren, die sich von dem realen Zustand der Plattform unterscheiden. Daher sind für den nächsten Aktualisierungsprozess (wenn diese posterioren Verteilungen als die prioren Verteilungen für die Aktualisierung betrachtet werden) die prioren Verteilungen zuverlässiger als die eingeführten Verteilungen in den empfohlenen Praktiken und die Unsicherheiten werden während des nächsten Aktualisierungsprozesses schrittweise reduziert.

In dieser Studie wird eine Methode vorgestellt, um die Wahrscheinlichkeitsverteilung unsicherer Parameter zu aktualisieren, wenn neue Informationen (Prüfergebnisse) verfügbar werden. Solche Informationen können verwendet werden, um die Wahrscheinlichkeitsverteilungen der unsicheren Parameter zu aktualisieren. Rissgröße, POD-Kurve, anfängliche Rissgröße, Risswachstumsparameter, Spannungsbereich und Geometriefunktion werden als unsichere Parameter betrachtet.

Die Ermüdungswahrscheinlichkeit des Versagens von Rohrverbindungen hängt von der Rissgrößenverteilung ab. Da die Rissgröße eine Funktion von mehreren Parametern ist, beeinflussen die Verteilungen dieser Parameter die Rissgrößenverteilung. Verschiedene Studien schlagen unterschiedliche Verteilungen für diese Parameter vor. Daher ist die Auswahl der geeigneten Prioritätsverteilungen entscheidend und manchmal schwierig. In dieser Studie wird ein Rahmenwerk entwickelt, um das Vorwissen über die unsicheren Parameter zu verbessern. Außerdem ist das Framework in der Lage, die Rissgrößenverteilung und die Ausfallwahrscheinlichkeit zu aktualisieren.

Die vorgeschlagene Methodik nutzt die Daten der Simulierten Realität, um zu verstehen, wie die vorherigen Annahmen mit den Beobachtungen kombiniert werden, um die posterioren Schätzungen des Bayes'schen Verfahrens zu verbessern. In dieser Studie werden Simulierte-Realitäts-Daten anstelle von realen Daten verwendet, da in der Regel nicht genügend reale Daten vorhanden sind, um das Verhalten der Methode zu überprüfen.

Die Sampling-Methode wird verwendet, um die Prior-Verteilung der Rissgrößen zu erzeugen. Eine große Anzahl von Zufallszahlen für jede Eingangsvariable wird auf Basis ihrer Verteilungen erzeugt. Die Rissgröße wird dann für jeden Satz von zufällig erzeugten Stichproben berechnet. Um die Simulierte-Realitäts-Verteilungen der Eingangsvariablen zu erhalten, wird außerdem das Konzept der äquivalenten anfänglichen Rissgrößenverteilung verwendet. Um die posteriore Verteilung zu erhalten, wird das Konzept der Kompatibilität definiert. Zu diesem Zweck wird jeder erkannte vorherige Riss mit jedem Simulierte-Realitäts-Riss verglichen. Wenn der Prior-Riss nahe an der Simulierten Realität liegt, wird er als kompatibler Prior angenommen, andernfalls wird er als inkompatibler Prior betrachtet. Die Posterior-Verteilung wird dann durch Entfernen der inkompatiblen Priors und Anpassen der besten Verteilung an die kompatiblen Priors erreicht.

Die Ergebnisse dieser Aktualisierungsmethode zeigen, dass sich die Posterior-Verteilungen der unsicheren Parameter in Richtung der Simulierte-Realitäts-Verteilung  verschieben. Es wird auch gezeigt, dass die Unsicherheit der posterioren Rissgrößenverteilung abnimmt, während die Unsicherheit der Eingangsvariablen zunimmt, da die Inspektionsergebnisse nur Daten über die Rissgröße enthalten und keine Informationen über die Eingangsvariablen liefern.

Die aktualisierten Verteilungen werden als die Prior-Verteilungen für den nächsten Aktualisierungsprozess verwendet, wenn neue Inspektionsergebnisse verfügbar sind.

Die der englischsprachigen Erstveröffentlichung zugrunde liegende Forschungsarbeit wurde durch die Förderung und Unterstützung der Lloyd's Register Foundation finanziert.

Die englischsprachige Erstveröffentlichung wurde durch das Sponsoring und die Unterstützung der Lloyd's Register Foundation möglich gemacht. Die Stiftung trägt zum Schutz von Leben und Eigentum bei, indem sie ingenieurbezogene Ausbildung, öffentliches Engagement und die Anwendung von Forschung unterstützt. Die Arbeit wurde durch das National Structural Integrity Research Centre (NSIRC) ermöglicht und durchgeführt, eine postgraduale technische Einrichtung für industriegeführte Forschung im Bereich der strukturellen Integrität, die vom TWI über ein Netzwerk von nationalen und internationalen Universitäten eingerichtet und geleitet wird.

Die Methodik wurde von Hadi Khalili und Nigel Barltrop zusammen mit Selda Oterkus und Ujjwal Bharadwaj entwickelt. Hadi Khalili führte die numerische Simulation durch.

Das englische Manuskript wurde von Hadi Khalili und Selda Oterkus geschrieben und von Selda Oterkus, Nigel Barltrop und Ujjwal Bharadwaj begutachtet. Alle Autoren haben die anschließend veröffentlichte englischsprachige Version des Manuskripts gelesen und ihr zugestimmt.

Stephan Kallee übersetzte den unter einer Creative Commons Lizenz lizensierten Open-Access-Artikel vom Englischen ins Deutsche. Die ursprünglichen Autoren waren daran nicht beteiligt.  

Die Autoren erklären keinen Interessenkonflikt. 

Der englische Open-Access-Artikel (Bild 10) wurde vom Lizenznehmer MDPI, Basel, Schweiz, in einer Sonderausgabe des J. Mar. Sci. Eng. 2020, 8(10), 778 unter einer Creative Commons Lizenz (Namensnennung 4.0 International, CC BY 4.0) wie folgt veröffentlicht (siehe Bild 20):

Hadi Khalili^<2><3>*, Selda Oterkus^<2>* Nigel Barltrop^<2>  und Ujjwal Bharadwaj^<4>: Updating the Distributions of Uncertain Parameters Involved in Fatigue Analysis

<2> Department of Naval Architecture, Ocean & Marine Engineering, University of Strathclyde, Glasgow G4 0LZ, UK

<3> National Structural Integrity Research Centre, TWI Ltd, Granta Park, Cambridge CB21 6AL, UK
<4> TWI Ltd., Granta Park, Great Abington, Cambridge CB21 6AL, UK

*Korrespondierende Autorin: selda.oterkus@strath.ac.uk; Tel.: +44-141-548-4979

DOI: https://www.mdpi.com/2077-1312/8/10/778

Jede weitere Verbreitung dieses Werkes muss die Autoren sowie den Titel des Werks, die Zeitschrift und den digitale Objektbezeichner (DOI) aufführen.

1. Heredia-Zavoni, E.; Montes-Iturrizaga, R. A Bayesian Model for the Probability Distribution of Fatigue. J. Offshore Mech. Arct. Eng. 2004, 126, 243–249. [Google Scholar] [CrossRef]
       
2. Karandikar, J.M.; Kim, N.H.; Schmitz, T.L. Prediction of remaining useful life for fatigue-damaged structures using Bayesian inference. Eng. Fract. Mech. J. 2012, 96, 588–605. [Google Scholar] [CrossRef]
      
3. Peng, T.; He, J.; Xiang, Y.; Liu, Y.; Saxena, A.; Celaya, J.; Goebel, K. Probabilistic fatigue damage prognosis of lap joint using Bayesian updating. J. Intell. Mater. Syst. Struct. 2015, 26, 965–979. [Google Scholar] [CrossRef]
      
4. Carr, P.; Busby, P.L.; Cresswell, S.M. A Unified Probabilistic Approach to Design & Inspection of Offshore Steel Structures. In Proceedings of the Third International Symposium on Integrity of Offshore Structures, Glasgow, UK, 28–29 September 1987; pp. 375–394. [Google Scholar]
      
5. DNV. Guideline for Structural Reliability Analysis: Application to Jacket Platforms; Report No. 95-3203; DNV: HØVIK, Norway, 1995. [Google Scholar]
      
6. JCSS. Fatigue Models for Metallic Structures; Joint Committee on Structural Safety: Aalborg, Denmark, 2011. [Google Scholar]
      
7. Siddiqui, N.A.; Ahmad, S. Fatigue and fracture reliability of TLP tethers under random loading. Mar. Struct. 2001, 14, 331–352. [Google Scholar] [CrossRef]
      
8. Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis, 2nd ed.; Chapman and Hall/CRC Press: New York, NY, USA, 2009. [Google Scholar]
      
9. Aghakouchak, A.A.; Stiemer, S.F. Fatigue reliability assessment of tubular joints of existing offshore structures. Can. J. Civ. Eng. 2001, 28, 691–698. [Google Scholar] [CrossRef]
      
10. Almar-Naess, A. Fatigue Handbook for Offshore Steel; Tapir Publication: Trondheim, Norway, 1985. [Google Scholar]
       
11. Etube, L.S. Fatigue and Fracture Mechanics of Offshore Structures; Professional Engineering Publishing Limited: London, UK, 2001. [Google Scholar]
       
12. Dover, W.D.; Dharmavasan, S. Fatigue and Fracture Mechanics Analysis of T and Y joints. In Proceedings of the Offshore Technology Conference, OTC 4404, Houston, TX, USA, 3–6 May 1982. [Google Scholar]
       
13. Lee, M.M.K.; Bowness, D. Stress intensity factors for weld toe cracks in tubular joints. In Proceedings of the Fifth International Conference on Engineering Structural Integrity Assessment, Cambridge, UK, 19–21 September 2000. [Google Scholar]
       
14. He, J.; Yang, J.; Wang, Y.; Waisman, H.; Zhang, W. Probabilistic Model Updating for Sizing of Hole-Edge Crack Using Fiber Bragg Grating Sensors and the High-Order Extended Finite Element Method. Sensors 2016, 16, 1956. [Google Scholar] [CrossRef] [PubMed]
       
15. DNV-GL SESAM Genie; V 7.4; Det Norske Veritas Software: Oslo, Norway, 2015.
        
16. Wirshing, P.H.; Light, M.C. Fatigue under wide band random stresses. ASCE J. Struct. Div. 1980, 106, 1593–1607. [Google Scholar]
       
17. Karadeniz, H. Uncertainty Modelling in the Fatigue Reliability Calculation of Offshore Structures. Reliab. Eng. Syst. Saf. 2001, 74, 323–335. [Google Scholar] [CrossRef]
       
18. BS 7910:2013. Guide to Methods of Assessing the Acceptability of Flaws in Metallic Structures, 3rd ed.; BSI: London, UK, December 2013. [Google Scholar]
       
19. Khalili, H.; Oterkus, S.; Barltrop, N.; Bharadwaj, U.; Tipping, M. System reliability calculation of jacket platforms including fatigue and extreme wave loading. Trends in the Analysis and Design of Marine Structures. In Proceedings of the 7th International Conference on Marine Structures, Marstruct, Dubrovnik, Croatia, 6–8 May 2019; Taylor & Francis Group: London, UK, 2015. [Google Scholar]
       
20. Lin, H.; Chen, G.; Wang, Z.; Yang, L. Integrality Assessment of Tubular Joints in Aging Offshore Platform Based on Reliability Theory. Adv. Mater. Res. 2012, 532–533, 238–242. [Google Scholar] [CrossRef]
       
21. Val, D. Safety, Risk and Reliability; Heriot-Watt University: Edinburgh, UK, 2014. [Google Scholar]
       
22. Python V.3.7. Available online: www.python.org (accessed on 3 October 2020).
       
23. Moan, T. Reliability-based management of inspection, maintenance, and repair of offshore structures. Struct. Infrastruct Eng. 2005, 1, 33–62. [Google Scholar] [CrossRef]
       
24. Kelly, D.; Smith, C. Bayesian Inference for Probabilistic Risk Assessment; Springer: Idaho Falls, ID, USA, 2011. [Google Scholar]
       
25. Rajasankar, J.; Iyer, N.R.; Appa Rao, T.V.S.R. Structural integrity assessment of offshore tubular joints based on reliability analysis. Int. J. Fatigue 2003, 25, 609–619. [Google Scholar] [CrossRef]
       
26. Rudd, J.L.; Gray, T.D. Quantification of fastener-hole quality. J. Aircr. 1978, 15, 143–147. [Google Scholar] [CrossRef]
       
27. Yang, J.N.; Manning, S.D. Statistical distribution of equivalent initial flaw size. In Proceedings of the Annual Reliability and Maintainability Symposium, San Francisco, CA, USA, 22–24 January 1980. [Google Scholar]